Knife Edge Test for Lens Evaluation

Introduction

Lens design is a constant quest to achieve optical perfection. Lenses and mirrors play crucial roles in imaging systems, but their imperfections can lead to optical aberrations, degrading the quality of images formed. One valuable tool that has stood the test of time for assessing and correcting these aberrations is the Foucault test, also known as the Knife Edge test. This technique provides a precise way to evaluate the surface quality of lenses and mirrors, ensuring that optical systems deliver high-quality performance.

Named after the French physicist Léon Foucault, this test has been an essential part of the optics engineer’s toolkit since its introduction in the mid-19th century. In this article, we will explore the principles, applications, and significance of the Foucault test in the evaluation of optical aberrations.

The Basics of the Foucault Test

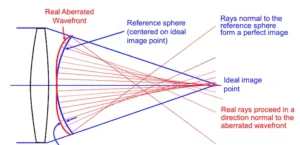
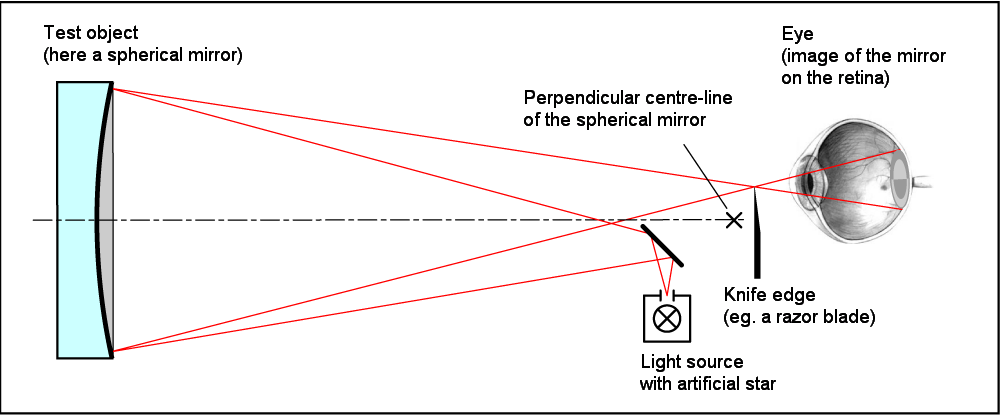
The Foucault test is a qualitative method for assessing the surface shape and optical quality of mirrors and lenses. It operates on the principle of comparing the behavior of light rays reflected or transmitted through the optical element under examination. The test setup typically involves a point light source placed at the focal point of the optical element, producing a diverging or converging beam. A knife-edge or flat opaque card is then positioned in the path of the light rays beyond the focus.

Principles of Operation

When the optical element is perfectly spherical or parabolic, the reflected or transmitted light rays converge to a point on the optical axis. As the knife-edge is moved across this focus, the intensity of light falling on a screen or detector changes gradually. This change in brightness is subtle, revealing minimal aberration.

However, if the optical element suffers from aberrations, the light rays will not converge to a precise point. Instead, they form a pattern known as an “interference pattern” or “shadowgram” on the detector/screen. The position and shape of this pattern can indicate the presence and type of aberration present in the optical element.

Types of Aberrations Revealed by the Foucault Test

1. Spherical Aberration: This common aberration occurs when light rays passing through the outer portions of the optical element focus at different points compared to the rays near the optical axis. In the Foucault test, this manifests as an uneven illumination pattern in the shadowgram.
2. Coma: Coma aberration causes off-axis light rays to form comet-like patterns instead of sharp points. These patterns are observed as curved lines in the Foucault test shadowgram.
3. Astigmatism: Astigmatism causes light rays in different meridians to focus at different distances. In the Foucault test, it appears as elliptical or oval-shaped zones in the shadowgram.
4. Higher-order aberrations: These are more complex aberrations that result in intricate patterns in the Foucault test shadowgram. They are combinations of different aberrations and can be challenging to interpret without additional analysis.

Applications of the Knife Edge Test

1. Telescope and Mirror Evaluation: The Foucault test is invaluable in testing and optimizing the shape of telescope mirrors and primary reflectors. It helps ensure that the optical elements meet the required specifications, leading to enhanced imaging performance.
2. Lens Production and Inspection: In lens manufacturing, the Foucault test aids in evaluating the surface quality of lenses, detecting potential manufacturing defects or aberrations, and ensuring consistency in performance.
3. Astronomical Observations: In astronomical observations, the Foucault test helps astronomers assess the quality of telescope mirrors and correct any aberrations that might affect the clarity of images captured.

Significance of the Foucault Test

The Foucault test’s enduring significance lies in its ability to provide a rapid, qualitative assessment of optical aberrations without the need for complex equipment or extensive analysis. It remains a valuable tool for optics engineers and astronomers, especially when precision optics are required for critical applications. Additionally, it serves as a crucial step in the iterative process of designing and fabricating optical elements, allowing engineers to refine and correct imperfections to achieve the desired performance.

Conclusion

The Foucault or knife edge test has withstood the test of time as a powerful tool for evaluating optical aberrations in mirrors and lenses. Through its qualitative analysis of interference patterns, it allows for the identification and correction of aberrations, leading to improved imaging quality. As advancements in technology continue, the Foucault test remains an essential part of the optics engineer’s arsenal, contributing to the ongoing pursuit of optical perfection in various scientific and industrial applications.